Quantitation: Statistical procedures
Usually, identification and quantitation are performed at the peptide level. The Mascot result report
assigns the peptide matches to protein hits, and the ratios for individual peptide matches are combined to
determine ratios for the protein hits. The methods provided for calculating a protein ratio
from a set of peptide ratios are median, average, or
weighted average. The standard deviation of the peptide ratios provides
a measure of the uncertainty in the protein ratio.
Since we are dealing with ratios, the average is the geometric mean
and the standard deviation is the geometric standard deviation, which is a factor.
In other words, the confidence interval is obtained by dividing and multiplying the average by the standard
deviation, which is never less than 1.0. For example, if the average is 0.91 and SD(geo) is
1.06 then the confidence interval is 0.86 to 0.96.
Ratios for peptide matches are only reported if various quality criteria are fulfilled,
the most important being:
- Peptide modification state
- Minimum precursor charge, (default 1)
- Strength of the peptide match, defined in terms of either a minimum score, a maximum
expect value, or the score being at or above either the identity threshold or the
homology threshold, (default maximum expect of 0.05)
- Method specific criteria, such as a minimum number of fragment ion pairs for
multiplex
A ratio for a protein hit is only reported if the minimum number of peptide matches,
is achieved, (default 2). If the ratios for the peptide
matches are not consistent with a sample from a normal distribution, the SD(geo) value is displayed
in italics, and should be treated with caution.
Testing for outliers and reporting a standard deviation for the protein ratio relies on the
peptide ratios being consistent with a sample from a normal distribution, (in log space). If the
peptide ratios do not appear to be from a normal distribution, this may indicate that
the values are meaningless, and something went systematically wrong with the
the analysis. On the other hand, it may indicate something interesting,
like the peptides have been mis-assigned and actually come from two
proteins with very different ratios, so that the distribution is bimodal.
Shapiro-Wilk W test
In the Shapiro-Wilk W test, the null hypothesis is that the sample is taken from a normal
distribution. This hypothesis is rejected if the critical value P for the test
statistic W is less than 0.05. The routine used is valid for sample sizes between
3 and 2000.
References:
- Royston, J. P., An Extension of
Shapiro and Wilk's W Test for Normality to Large Samples, Applied Statistics 31 115-124 (1982)
- Royston, P., Remark AS R94: A
Remark on Algorithm AS 181: The W-test for Normality, Applied Statistics 44 547-551 (1995)
The available methods for testing and removing outliers are none, auto, dixons, grubbs, and rosners.
Choosing auto means that Dixon's method will be used if the number of values is between 4 and 25,
while Rosner's method will be used if the number of values is greater than 25. If the ratios for the peptide
matches are not consistent with a sample from a normal distribution, the SD(geo) value is displayed
in italics, and outlier removal is skipped.
Any statistician will advise of the dangers of blindly removing outliers. The general advice
is to analyze the data both with and without the outlier(s) and see if the conclusions are
qualitatively different.
Dixon's method
Dixon's r11 test, also referred to as N9, is used to detect and remove a single outlier at a time
from either the upper or lower extreme of the range. Critical values for a significance level 0.05
are used, as tabulated by Verma and Quiroz-Ruiz. The test is applicable to between 4 and 100 values.
Each time a value is removed, the test is repeated.
References:
- Dixon, W. J., Processing Data
for Outliers, Biometrics 9 74-89 (1953)
- Verma, S. P. and
Quiroz-Ruiz, A., Critical values for six Dixon tests for outliers in normal samples up to sizes
100, and applications in science and engineering, Revista Mexicana de Ciencias Geológicas, 23
133-161 (2006)
Grubbs' method
Grubbs' method is used to detect and remove a single outlier at a time
from either the upper or lower extreme of the range. Critical values for a significance level 0.05
are used, as tabulated by Verma and Quiroz-Ruiz (Table A1 for discordancy test N1). The test is
applicable to between 3 and 100 values. Each time a value is removed, the test is repeated.
References:
- Grubbs, F. E., Procedures for
Detecting Outlying Observations in Samples, Technometrics 11 1-21 (1969)
- Verma,
S. P. and Quiroz-Ruiz, A., Critical values for 22 discordancy test variants for outliers in
normal samples up to sizes 100, and applications in science and engineering, Revista Mexicana
de Ciencias Geológicas, 23 302-319 (2006)
Rosner's method
Rosner's method will detect and remove multiple outliers in a single pass.
Critical values for a significance level 0.05 are used. The test will remove up to 10 outliers
from a sample of at least 25 values.
References:
- Rosner, B., Percentage Points
for a Generalized ESD Many-Outlier Procedure, Technometrics 25 165-172 (1983)
The three methods of deriving a protein hit ratio from a set of peptide ratios are median, average,
and weighted.
- Median: The median peptide ratio is selected to represent the protein ratio. If
there are an even number of peptide ratios, the geometric mean of the median pair is used
- Average: The protein ratio is the geometric average of the peptide ratios
- Weighted: For each component, the intensity values of the set of peptides are summed
and the protein ratio(s) calculated from the summed values. This gives a weighted average,
which will be the best measure if the accuracy is limited by counting statistics. When a
weighted average is reported, the standard deviation is the weighted standard deviation. This
is the geometric standard deviation divided by the square root of the
effective
base.
A protein ratio is reported in bold face if it is significantly different from unity.
The comparison test is:
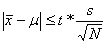
If this inequality is true, then there is no significant difference at the stated confidence level.
(N is the number of peptide ratios, s is the standard deviation and x the mean of
the peptide ratios, both numbers calculated in log space. The true value of the ratio, µ, is
0 in log space. t is students t for N-1 degrees of freedom and a two-sided confidence
level of 95%.)
Data normalisation strongly influences which protein ratios are shown in bold. If a large number
of values are bold, this is likely to indicate that the comparison to unity has no meaning. If the ratios for the peptide
matches are not consistent with a sample from a normal distribution, the SD(geo) value is displayed
in italics, and the significance test is omitted.
|